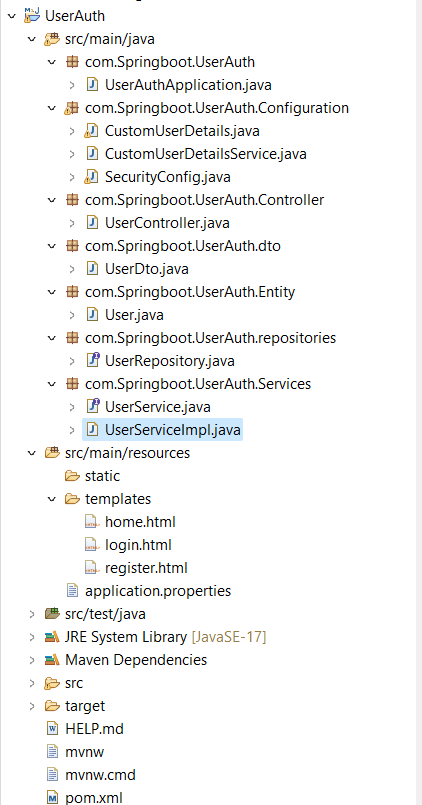
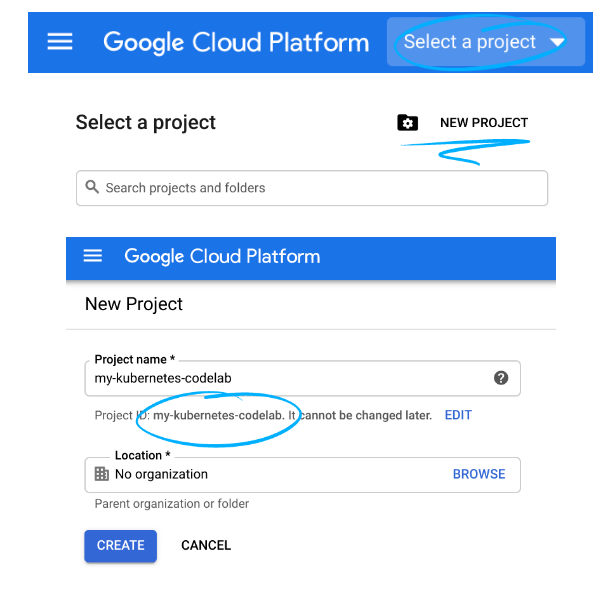
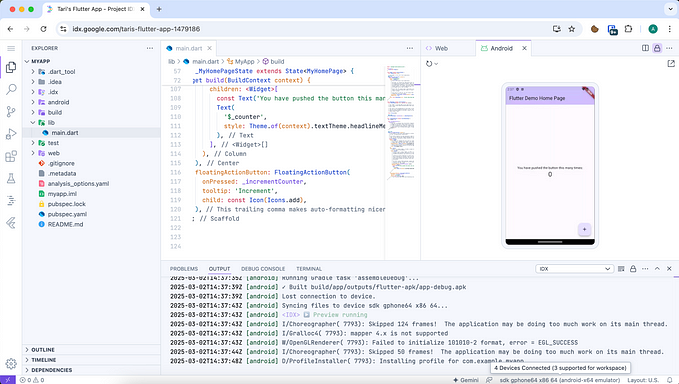
Boats and Streams Important Shortcuts And Tricks Explained with Examples…!

Stream:-
The moving water of the river is called a stream.
Still Water:-
If the water is not moving then it is called still water.
upstream:-
If a boat or a swimmer moves in the opposite direction of the stream then it is called upstream.
Downstream:-
If a boat or a swimmer moves in the same direction of the stream then it is called downstream.
Points to remember:-
i. When the speed of a boat or a swimmer is given then It normally means speed in still water.
ii. If the speed of the boat or swimmer is x km/h and the speed of the stream is y km/h then, The Speed of the boat or swimmer upstream = (x — y) km/h, the Speed of the boat or swimmer downstream = (x + y) km/h
iii. The speed of the boat or swimmer in still water is given by = 1/2(Downstream + Upstream)
The speed of the stream is given by = 1/2(Downstream — upstream)
Some Shortcut Methods:-
Trick-1:-
A man can row a certain distance downstream in tl hours and return the same distance upstream in t2 hours. If the speed of the stream is y km/h, then the speed of man in still water is given by =y*(t2+t1)/(t2-t1).
Ex: A man can row a certain distance downstream in 2 hours and return the same distance upstream in 4 hours. If the speed of a stream is 5 km/h, then the speed of man in still water?
a. 15 b. 10 c. 12 d.20
sol: =5*(4+2)/(4–2)=≥5*(6)/(2)=>5*3= 15 km/hr.
Trick-2:-
A man can row a certain distance downstream in tl hours and return the same distance upstream in t2 hours. If the speed of the stream is y km/h, then the speed of man in still water is given by = y*(t2-t1)/(t2+t1).
Ex: Ramesh can row a certain distance downstream in 6 hours and return the same distance in 9 hours. If the speed of Ramesh in still water is 12 kmph. Find the speed of the stream.
a. 2.4 b. 10 c. 1.2 d. 20
Sol: Speed of the stream =12 ( 9–6) /(9+6) =>12*(3)/15 = 2.4 kmph.
Trick-3:-
A man can row in still water at x km/h. In a stream flowing at y km/h, if it takes him ‘t’ hours to row to a place and come back, then the distance between two places is given by = [t*(x²-y²)]/(2*x).
Ex: A man can row in still water at 4 km/h. In a stream flowing at 2 km/h, if it takes him ‘5’ hours to row to a place and come back, then the distance between two places?
a. 15 b. 10 c. 12 d. 7.5
sol : =[5*(4²-2²)]/(2*4) => [5*(16–4)]/8 =>[5*(12)]/8=>7.5km.
Trick-4:-
A man can row in still water at x km/h. In a stream flowing at y km/h, if it takes t hours more in upstream than to go downstream for the same distance, then the distance is given by =[t*(x²-y²)]/(2*y).
Ex: A man can row in still water at 4 km/h. In a stream flowing at 2 km/h, if it takes 3 hours more in upstream than to go downstream for the same distance, then the distance swims by person ?
a. 15 b. 9 c. 12 d. 7.5
sol: =[3*(16–4)]/(2*2) =>[3*(12)]/4 =>9 km.
Trick-5:-
A man can row in still water at x km/h. In a stream flowing at y km/h, if he rows the same distance up and down the stream, then his average speed is given by (x²-y²)/(x). = (Downstream • Upstream)/man speed in still water.
Ex: A man can row in still water at 4 km/h. In a stream flowing at 2 km/h, if he rows the same distance up and down the stream, then his average speed
a. 6 b. 9 c. 3 d. 7.5
sol: (16–4)1/4= 3 km/hr.
Trick-6:-
A man can row a distance ‘D’ upstream in t1 hrs. If he rows the same distance down the stream in t2 hrs. then speed is given by Stream speed =[D*(t1-t2)]/(2*t1*t2).
Ex: A man can row a distance 30 km upstream in 5 hrs. If he rows the same distance down the stream in 3 hrs. then the speed of stream?
a.8 b. 4 c. 2 d. 6
sol: [30*(5–3)]/(2*5*3) => (30*2)/(30) => 2km/hr.
Trick-7:-
A man can row a distance ‘D’ upstream in tl hrs. If he rows the same distance down the stream in t2 hrs. then speed is given by Man speed =[D*(t1+t2)]/(2*t1*t2).
Ex: A man can row a distance 30 km upstream in 5 hrs. If he rows the same distance down the stream in 3 hrs. then the speed of man?
a. 8 b. 4 c. 2 d. 6
sol: [30*(5+3)]/(2*5*3) => (30*8)/(30) => 8km/hr.
Conclusion:-
This article gives some important tricks that you can use to practice related problems. thanks for reading. please follow Ram.